Вычислительная геометрия.Часть 1

«Вычислительная геометрия – это раздел информатики, изучающий алгоритмы решения геометрических задач. Такие задачи возникают в компьютерной графике, проектировании интегральных схем, технических устройств и др. Исходными данными в такого рода задачах могут быть множество точек, набор отрезков, многоугольники и т.п. Результатом может быть либо ответ на какой-то вопрос, либо какой-то геометрический объект».

Поскольку статья является достаточно большой я решил разбить ее на две части: первая часть посвящена многоугольникам, вторая – взаимному расположению различных геометрических объектов.

Немного теории о векторах

Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет

какого-либо определенного направления. Длиной ненулевого вектора AB называется длина отрезка AB. Длина нулевого вектора считается равной нулю. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два ненулевых вектора AB и CD коллинеарны и если при этом лучи AB и CD сонаправлены, то векторы AB и CD называются сонаправленными, а если эти лучи не являются сонаправленными, то векторы AB и CD называются противоположно направленными. Нулевой вектор принято считать сонаправленным с любым вектором.

Скалярное произведение векторов

Скалярное произведение векторов — это число, равное произведению длин этих векторов на












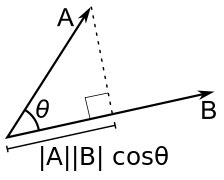
косинус угла между ними. (a, b) = |a||b|cos∠(a, b) Если векторы заданы своими координатами a(x₁, y₁), b(x₂, y₂) то скалярное произведение (a, b) = x₁x₂ + y₁y₂.

Косое произведение векторов

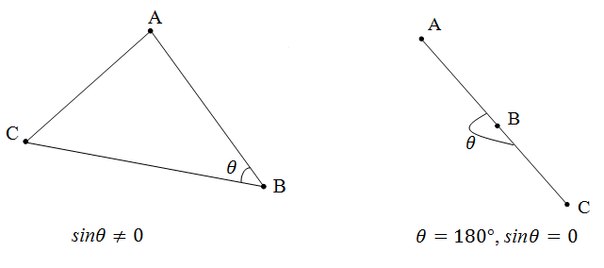
Псевдоскалярным или косым произведением векторов на плоскости называется число [a, b] = |a||b|sinθ где — угол вращения (против часовой стрелки) от a к b. Если хотя бы один из векторов a и b нулевой, то полагают [a, b] = 0. Если векторы заданы своими координатами a(x₁, y₁), b(x₂, y₂) то косое произведение [a, b] = x₁y₂ - x₂y₁. Геометрически косое произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора. Косое произведение векторов в задачах вычислительной геометрии занимает такое же почетное место, как рекурсии в комбинаторике. Это своего рода жемчужина вычислительной геометрии. Практически каждая задача вычислительной геометрии имеет более простое решение с помощью косового произведение вместо лобового решения.

А теперь займемся практикой...

Задача №1

Задача очень простая, а именно: по введенным трем числам a, b, c определить существует ли треугольник с такими сторонами.

Решение: Понятно, что здесь нужно только проверить неравенство треугольника: a + b > c, a + c > b, b + c > a. Интересно, при изучении неравенства треугольника только ли у меня возник вопрос: не могут ли отрицательные числа тоже удовлетворять этим трем неравенствам? Оказывается, нет! Если мы сложим каждое неравенство, то получим a > 0, b > 0, c > 0. Поэтому неравенство треугольника является необходимым и достаточным условием существования треугольника.

Задача №2

Задача является очень похожей на предыдущую с той разницей, что треугольник задан не сторонами, а координатами вершин.

Решение: С первого взгляда решение кажется очевидным: вычислить стороны треугольника и свести задачу к предыдущей. Однако поскольку расстояние между двумя точками A(x₁, y₁), B(x₂, y₂) вычисляется по формуле √(x₁-x₂)²+(y₁-y₂)² то при извлечении корня возможна потеря точности, что плохо скажется на проверке неравенства треугольника. Оказывается, что если треугольник задан координатами своих вершин, то вычислять длины его сторон и проверять неравенство треугольника не требуется. В этом случае треугольника не существует тогда и только тогда, когда данные три точки лежат на одной прямой. А это легко проверяется через косое произведение векторов. Если оно равно нулю, то векторы коллинеарные, то есть все три точки лежат на одной прямой.
Во всех следующих задачах будем считать, что треугольник существует, поскольку процедуру проверки существования треугольника мы только что рассмотрели.

Задача №3

Треугольник задан своими сторонами. Определить тип треугольника: тупоугольный, прямоугольный или остроугольный.

Решение: Вспомним, что представляют собой каждый вид треугольника. 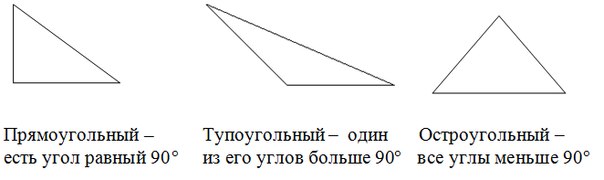Из курса геометрии известно, что напротив большей стороны лежит больший угол (он нам и нужен). Поэтому если мы выясним чему равен больший угол, то поймем тип треугольника:

1. Угол больше 90° – треугольник тупоугольный
2. Угол меньше 90°– треугольник остроугольный
3. Угол равен 90°– треугольник прямоугольный

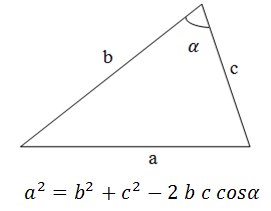
Воспользуемся теоремой косинусов: Очевидно, что если косинус угла больше нуля то угол меньше 90°, если он равен нулю, то угол равен 90°, если он меньше нуля, то угол больше 90°. Однако немного поразмыслив можно понять, что вычислять косинус угла не обязательно, необходимо учесть лишь его знак:

• Если cosα > 0, то a² < b² + c² – треугольник остроугольный
• Если cosα = 0, то a² = b² + c² – треугольник прямоугольный
• Если cosα < 0, то a² > b² + c² – треугольник тупоугольный

где a – большая сторона.

Задача №4

Задача аналогична предыдущей задаче, только треугольник задан не своими сторонами, а координатами вершин.

Решение: Аналогично задаче 2 можно сказать, что эта задача полностью сводится к предыдущей задаче (так оно и есть). Однако, как и во второй задаче, решение можно упростить. Вообще, если треугольник задан координатами своих вершин, то всегда легче работать с ним через вектора, нежели вычислять стороны. Аналогично предыдущей задаче, необходимо определить каким является наибольший из углов треугольника. Вид угла легко определяется по знаку скалярного произведения образующих его векторов: оно положительно для острого угла, равно нулю для прямого угла и отрицательно для тупого угла. Поэтому необходимо посчитать все три скалярных произведения и перемножить их и по знаку данного числа можно судить о типе треугольника.

Задача №5

По данным сторонам треугольника найти его площадь.

Решение: Очевидно решение, заключается в применение формулы Герона.

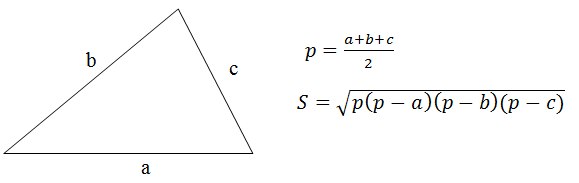
Кстати, никого не интересовало доказательство этой формулы?
   

Задача №6

Вычислить площадь треугольника заданного координатами своих вершин.

Решение: Не будем говорить о решении, которое сводится к предыдущей задачи, а попробуем воспользоваться геометрическим смыслом косового произведения. Геометрически косое произведение двух векторов определяет ориентированную площадь параллелограмма натянутого на эти вектора. Поскольку диагональ параллелограмма разбивает его на два равновеликих треугольника, то можем найти площадь нашего треугольника, как половину площади параллелограмма. Для векторов a(x₁, y₁), b(x₂, y₂) S = (x₁y₂ - x₂y₁) / 2 - ориентированная площадь треугольника

Задача №7

Дана точка и треугольник заданный координатами своих вершин. Определить лежит ли точка внутри, на границе или вне этого треугольника.

Решение: У этой задачи есть два принципиально разных решения. Начнем с наименее привлекательного.

Метод площадей

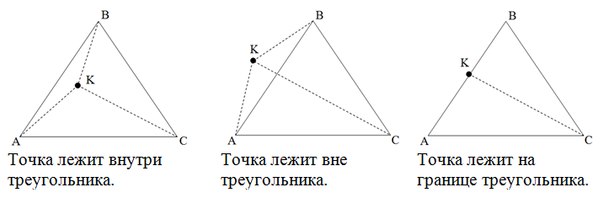
Если сумма площадей треугольников AKB, AKC, BKC (не ориентированных, а «обычных») больше площади треугольника ABC точка лежит вне треугольника. Если же сумма первых трех площадей равна четвертой, то нужно проверить, не равна ли нулю одна из трех площадей. Если равна, то точка лежит на границе треугольника, иначе – внутри. Вычислять площади треугольников, естественно, надо через косое произведение векторов. Этот метод не очень хороший. Поскольку здесь используются сравнение чисел с плавающей точкой, а это в свою очередь может привести к принятию неверного решения при сравнении. Второй метод опять таки опирается на вектора, он намного эффективнее во всех отношениях.

Проверка полуплоскостей

Если хотя бы одна из сторон треугольника «разводит» противолежащую ей вершину и точку по разным полуплоскостям, то точка лежит вне треугольника. Иначе, если точка принадлежит хотя бы одной из прямых, содержащих стороны треугольника, то она находится на границе треугольника. Иначе точка лежит внутри треугольника.
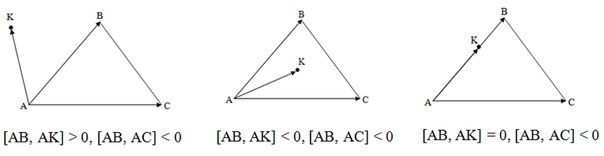
 В первом примере сторона AB разводит вершину C и точку K по разным полуплоскостям, поэтому точка лежит снаружи.

Задача №8

Вычисление площади многоугольника заданного координатами своих вершин.

Решение: Под многоугольником будем подразумевать простой многоугольник, то есть без самопересечений. При этом он может быть как выпуклым, так и не выпуклым. Данную задачу можно решить двумя способами: вычисляя ориентированные площади трапеций и треугольников.

Метод трапеций

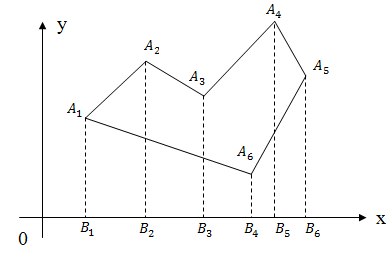
Для того чтобы посчитать площадь многоугольника нужно разбить его на трапеции, так как это показано на рисунке, а затем сложить ориентированные площади полученных трапеций это будет ориентированной площадью исходного многоугольника. S = S_{A1 A2 B2 B1} + S_{A2 A3 B3 B2} + S_{A3 A4 B5 B3} + S_{A4 A5 B6 B5} + S_{A5 A6 B4 B6} + S_{A6 A1 B1 B4} Площади трапеций считаем по известной формуле: полусумма оснований на высоту S_{A1 A2 B2 B1} = 0.5 * (A₁B₁ + A₂B₂) *(B₂ - B₁) Поскольку полученная площадь является ориентированной, необходимо вычислить ее модуль.

Метод треугольников

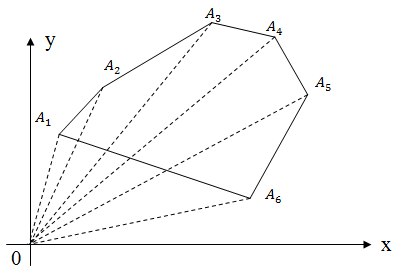
 Аналогично предыдущему методу можно разбивать многоугольник не на трапеции, а на треугольники, как показано на рисунке. В результате, сложив ориентированные площади этих треугольников, мы получим опять-таки ориентированную площадь многоугольника. S = S_OA1A2 + S_OA2A3 + S_OA3A4 + S_OA4A5 + S_OA5A6 + S_OA6A1 Как вы видите задача вычисления площади многоугольника достаточна проста. Не знаю, почему, но мне больше нравится решать эту задачу методом разбиения на трапеции (наверно потому, что на всех олимпиадах я ее так решал). Тем более, что при втором решении площади треугольников надо вычислять через косое произведение. О формуле Герона надо забыть!!!

Задача №9

Многоугольник задан координатами своих вершин в порядке его обхода. Необходимо проверить является ли многоугольник выпуклым.

Решение: Напомню, что многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.

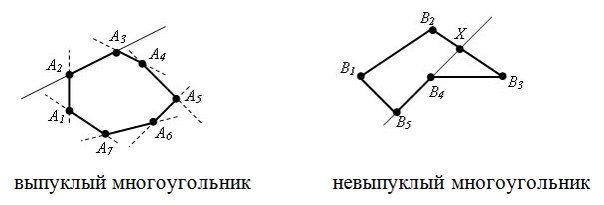
 Задача опять сводится к вычислению косового произведения векторов, а именно у выпуклого многоугольника знаки косых произведений [A_i A_i+1, A_i+1 A_i+2] либо положительны, либо отрицательны. Поэтому если мы знаем направление обхода, то знак косых произведений для выпуклого многоугольника одинаков: он неотрицателен при обходе против часовой стрелки и неположителен при обходе по часовой стрелки.

Задача №10

Многоугольник (не обязательно выпуклый) на плоскости задан координатами своих вершин. Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).

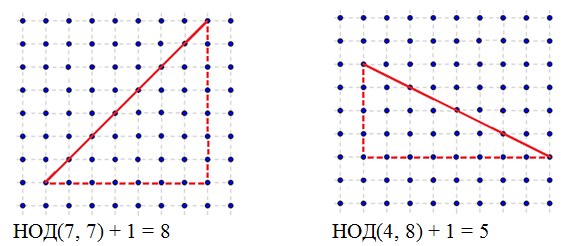
Решение: Для решения этой задачи рассмотрим вспомогательную задачу: отрезок задан координатами своих концов, являющихся целыми числами. Необходимо посчитать количество целочисленных точек лежащих на отрезке. Понятно, что если отрезок вертикальный или горизонтальный, то необходимо вычесть координаты концов и добавить единицу. Интерес представляет случай, когда отрезок не является вертикальным или горизонтальным. Оказывается в этом случае необходимо достроить отрезок до прямоугольного треугольника и ответом будет число равное наибольшему общему делителю длин катетов этого треугольника плюс единица.

 Для любого многоугольника с целочисленными координатами вершин справедлива формула Пика: S = n + m/2 - 1 , где S – площадь многоугольника, n – количество целых точек лежащих строго внутри многоугольника, m – количество целых точек лежащих на границе многоугольника. Поскольку площадь многоугольника мы знаем как вычислять, то S известно. Так же мы можем вычислить количество целых точек лежащих на границе многоугольника, поэтому в формуле Пика остается лишь одна искомая неизвестная которую мы можем найти.




















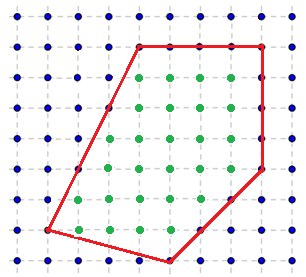
Рассмотрим пример: S = 16 + 4 + 4,5 + 6 + 1 + 2 = 33,5; m = 15; n = 33,5 – 7,5 +1 = 27 - точек лежит строго внутри многоугольника Вот так вот решается эта задачка!

 Вот и все!